二叉树的公共祖先

问题陈述

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

说明

  • 所有节点的值都是唯一的。
  • p、q 为不同节点且均存在于给定的二叉树中。

思路分析

递归解析：

终止条件：
当越过叶节点，则直接返回 null ；
当 root 等于 p, q，则直接返回 root ；

递推工作：
开启递归左子节点，返回值记为 left ；
开启递归右子节点，返回值记为 right ；

返回值： 根据 left和 right ，可展开为四种情况；
当 left和 right 同时为空 ：说明 root 的左 / 右子树中都不包含 p,q，返回 null；
当 left和 right 同时不为空 ：说明 p, q分列在 root的 异侧 （分别在 左 / 右子树），因此 root为最近公共祖先，返回 root；
当 left 为空 ，right 不为空 ：p,q都不在 root的左子树中，直接返回 right。具体可分为两种情况：
p,q其中一个在 root的 右子树 中，此时 right 指向 p（假设为 p）；
p,q两节点都在 root 的 右子树 中，此时的 right指向 最近公共祖先节点 ；
当 left不为空 ， right为空 ：与情况 3. 同理；

代码实现

1
2
3
4
5
6
7
8
9
10
11
class solution{
    public TreeNode getCommenParent(TreeNode root,TreeNode p,TreeNode q){
        if(root==null||root==p||root==q) return root;
        TreeNode left=getCommenParent(root.left,p,q);//在左子结点找到p
        TreeNode right=getCommenParent(root.right,p,q);//在右子结点找到p
        if(left==null) return right;
        if(right==null) return left;
        if(left==null&&right==null) return null;
        return root;//left!=null&&right!=null
    }
}

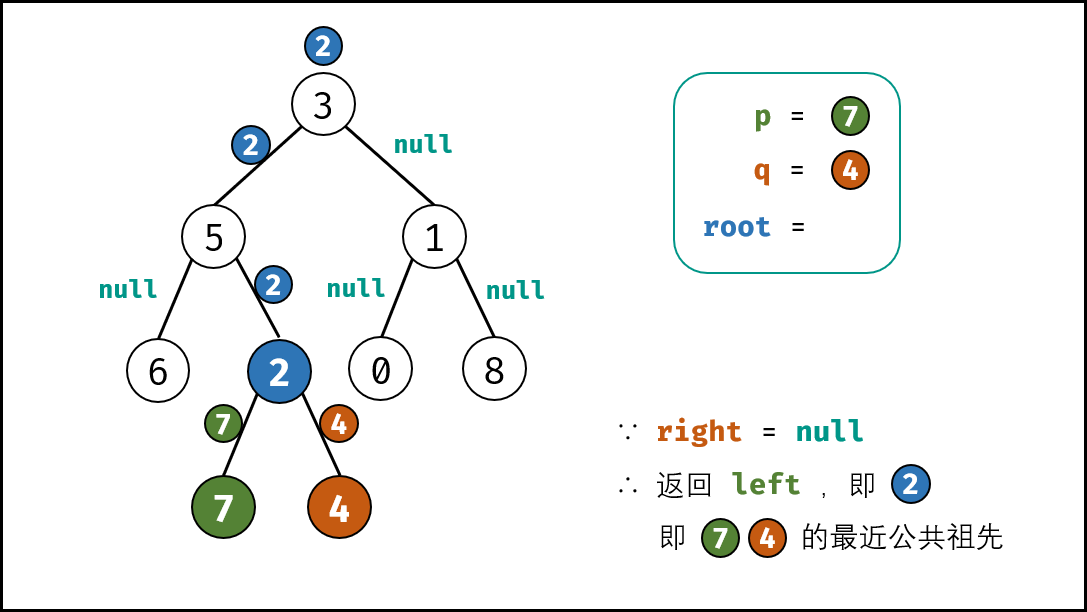
代码的执行及返回过程见上图，顺序3——5——6——2——7（返回left=7）——4（返回right=4）——（left！=null&&right！=null）返回root=2——（left=null）返回right=2——1——0——8——（返回null）——（right=null）返回left=2。即最终结点。