排序算法总结

排序算法汇总

冒泡排序

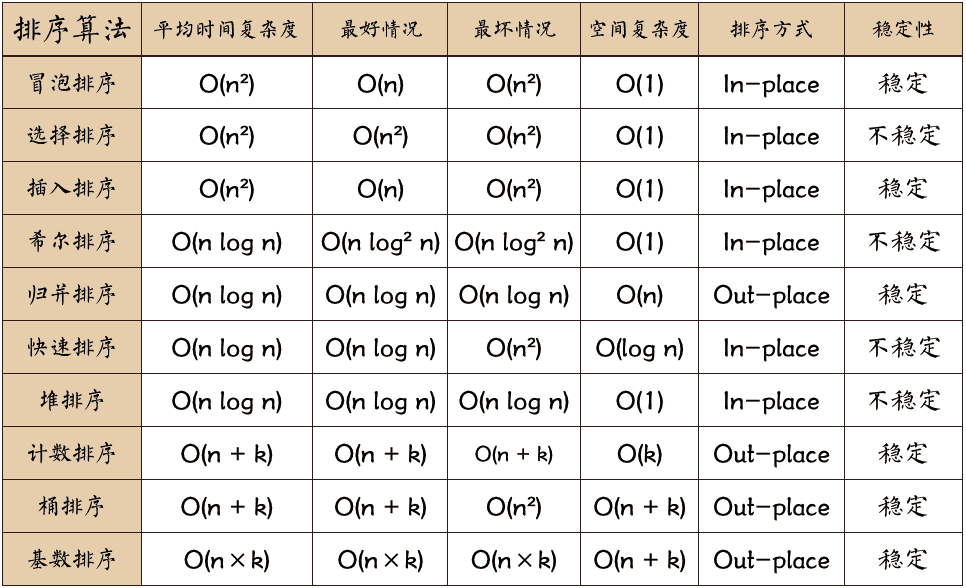
思路：俩俩交换，大的放在后面，第一次排序后最大值已在数组末尾。需要n-1次排序。

public class BubbleSort {
    public void bubbleSort(int[] array){
        //装载临时变量
        int temp;
        //记录是否发生了置换，0，没有置换；1，置换了。
        int isChange;
        //记录执行次数
        int count=0;
        //外层循环表示排序的趟数
        for(int i=0;i<array.length-1;i++){
            //每排序一趟就重新初始化为0
            isChange=0;
            //内层循环表示当前趟需要比较的次数
            for(int j=0;j<array.length-i-1;j++){
                //两两比较，前大于后，则交换。
                if(array[j]>array[j+1]){
                    temp=array[j];
                    array[j]=array[j+1];
                    array[j+1]=temp;
                    //发生了置换
                    isChange=1;
                }
            }
            //如果该趟排序未发生置换，说明后面有序，不必走完所有趟。
            if(isChange==0){
                break;
            }
            count++;
        }
        //打印输出排序后的序列
        for(int c:array)
            System.out.print(c+" ");

    }
    public static void main(String[] args){
        int[] array={2,6,1,9,3,5};
        BubbleSort bubbleSort=new BubbleSort();

        bubbleSort.bubbleSort(array);
    }
}

选择排序

思路：找到数组中最大的元素，与数组最后一位元素交换。当只有一个数时，则不需要选择了，因此需要n-1趟排序。

public class SelectSort {
    public void selectSort(int[] array){
        //记录当前趟数最大值的角标
        int pos;
        //外层循环
        for(int i=0;i<array.length-1;i++){
            //每趟pos重新置0
            pos=0;
            //内层循环得到该趟最大值
            for(int j=0;j<array.length-i;j++){
                if(array[j]>array[pos]){
                    pos=j;
                }
            }
            //该趟最大值与最后一个数交换
            int temp=array[pos];
            array[pos]=array[array.length-i-1];
            array[array.length-i-1]=temp;
        }
        for(int c:array)
            System.out.print(c+" ");
    }
    public static void main(String[] args){
        int[] array={1,3,7,4,2};
        SelectSort selectSort=new SelectSort();
        selectSort.selectSort(array);
    }
}

插入排序

思路：将一个元素插入到已有序的数组中，在初始时未知是否存在有序的数据，因此将元素第一个元素看成是有序的。与有序的数组进行比较，比它大则直接放入，比它小则移动数组元素的位置，找到个合适的位置插入。当只有一个数时，则不需要插入了，因此需要n-1趟排序。

public class InsertSort {
    public void insertSort(int[] array){
        //外层循环控制排序趟数，从1开始是因为把第0位视作有序
        for(int i=1;i<array.length;i++){
            int temp=array[i];
            //如果前一位（已排序的数据）比当前数据大，则进行循环比较后归为有序
            int j=i-1;
            while (j>=0&&array[j]>temp){
                array[j+1]=array[j];
                j--;
            }
            array[j+1]=temp;

        }
        for(int c:array)
            System.out.print(c+" ");

    }
    public static void main(String[] args){
        int[] array={3,6,2,8,7};
        InsertSort insertSort=new InsertSort();
        insertSort.insertSort(array);
    }
}

快速排序

思路：在数组中找一个元素(节点)，比它小的放在节点的左边，比它大的放在节点右边。一趟下来，比节点小的在左边，比节点大的在右边。不断执行这个操作。

public class QuickSort {
    public void quickSort(int[] array,int L,int R){
        int i=L;
        int j=R;
        //支点
        int pivot=array[(L+R)/2];
        while (i<j){
            //寻找比支点小的数
            while (pivot<array[j]){
                j--;
            }
            //寻找比支点大的数
            while (pivot>array[i]){
                i++;
            }
            //将右边比支点小的数与左边比支点大的数进行交换
            if(i<=j){
                int temp=array[i];
                array[i]=array[j];
                array[j]=temp;

                i++;
                j--;
            }
        }
        //上述while循环之后，完成了第一轮划分，j指向了pivot-1，i指向了pivot+1
        if(L<j){
            quickSort(array,L,j);
        }
        if(R>i){
            quickSort(array,i,R);
        }
    }

    public static void main(String[] args){
        int[] array={4,2,6,5,9};
        QuickSort quickSort=new QuickSort();
        quickSort.quickSort(array,0,array.length-1);
        for(int c:array)
            System.out.print(c+" ");
    }
}

归并排序

思路：将两个已排好序的数组合并成一个有序的数组,称之为归并排序。

public class MergeSort {
    //mergerSort 划分原数组
    
   // static方法就是没有this的方法。在static方法内部不能调用非静态方法，反过来是可以的。而且可以在没有创建任何对象的前提下，仅仅通过类本身来调用static方法。这实际上正是static方法的主要用途。(简而言之)方便在没有创建对象的情况下来进行调用（方法/变量）。
    public static void mergeSort(int[] array,int L,int R){
        //如果只有一个元素，直接返回
        if(L==R) return;
        else {
            int M=(L+R)/2;
            mergeSort(array,L,M);
            mergeSort(array,M+1,R);
            merge(array,L,M+1,R);
        }
    }
    //归并
    public static void merge(int[] array,int L,int M,int R){
        //定义左右数组，并分别存储array元素。
        int[] leftArray=new int[M-L];
        int[] rightArray=new int[R-M+1];
        for(int i=L;i<M;i++){
            leftArray[i-L]=array[i];
        }
        for(int i=M;i<=R;i++){
            rightArray[i-M]=array[i];
        }
        //左右数组比较，小的放入新的array。
        int i=0,j=0,k=L;
        while (i<leftArray.length&&j<rightArray.length){
            if(leftArray[i]<rightArray[j]){
                array[k]=leftArray[i];
                k++;
                i++;
            }else {
                array[k]=rightArray[j];
                k++;
                j++;
            }
        }
        //左数组元素还没比完，直接放入array
        while(i<leftArray.length){
            array[k]=leftArray[i];
            k++;
            i++;
        }
        //右数组元素还没比完，直接放入array
        while(j<rightArray.length){
            array[k]=rightArray[j];
            k++;
            j++;
        }

    }
    public static void main(String[] args){
        int[] array={3,1,7,5,4};
        MergeSort ms=new MergeSort();
        ms.mergeSort(array,0,array.length-1);
        for(int c:array)
            System.out.print(c+" ");
    }
}

堆排序

public class HeapSort {
    public static void main(String[] args){
        int[] arrays={2,8,4,6,9};
        maxheapify(arrays,arrays.length-1);
        int size=arrays.length-1;
        for(int i=0;i<arrays.length;i++){
            //将当前堆顶元素（最大值）交换到数组倒数第一位、第二位、……
            int temp=arrays[0];
            arrays[0]=arrays[arrays.length-1-i];
            arrays[arrays.length-1-i]=temp;
            //
            heapify(arrays,0,size);
            size--;
        }
        for(int c:arrays)
            System.out.print(c+" ");
    }
    //建堆
    public static void heapify(int[] arrays,int currentrootnode,int size){
        if(currentrootnode<size){
            int left=currentrootnode*2+1;//当前结点的左子结点索引
            int right=currentrootnode*2+2;//当前结点的右子结点索引

            int max=currentrootnode;//最大值结点索引初始化为当前结点
            if(left<size){
                if(arrays[max]<arrays[left]){//若当前结点值小于左子结点，则最大值结点索引=left
                    max=left;
                }
            }
            if(right<size){
                if(arrays[max]<arrays[right]){//若当前结点值小于左子结点，则最大值结点索引=right
                    max=right;
                }
            }
            if(max!=currentrootnode){ //如果最大值结点索引不等于当前结点索引，交换最大值结点为当前结点
                int temp=arrays[max];
                arrays[max]=arrays[currentrootnode];
                arrays[currentrootnode]=temp;

                heapify(arrays,max,size);//
            }
        }
    }
    //完成一次建堆
    public static void maxheapify(int[] arrays,int size){
        for(int i=size-1;i>=0;i--){
            heapify(arrays,i,size);
        }
    }
}