不同路径
问题陈述
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
问总共有多少条不同的路径?
思路分析
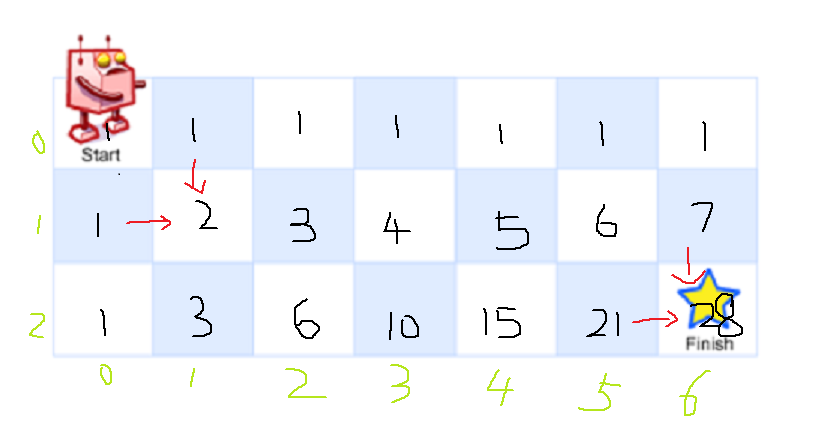
分析题意可知,机器人只能往下或右移动,也就是说当前格等于其左与其上的和。
转换为起点到终点的路径的话,则很明显,第一行和第一列的格子值都为1,也就是到达该格的路径只有一条,从左边来或从上边来。而对于中间的格子,可从左或上,格子值也就是可能的路径数等于左边加上边之和。
问题求解
代码一:
1
2
3
4
5
6
7
8
9
10
11
12
13
| class Solution{
public int uniquePaths(int m,int n){
int[][] mn=new int[m][n];
for(int i=0;i<n;i++) mn[0][i]=1;
for(int j=0;j<m;j++) mn[j][0]=1;
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
mn[i][j]=mn[i-1][j]+mn[i][j-1];
}
}
return mn[m-1][n-1];
}
}
|
代码二:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| class Solution {
public int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (i == 0 || j == 0)
dp[i][j] = 1;
else {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
}
return dp[m - 1][n - 1];
}
}
|


