完全平方数

问题陈述

给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, ...）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。

1
2
3
输入: n = 12
输出: 3 
解释: 12 = 4 + 4 + 4.

常规思路

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public int numSquares(int n) {
    return numSquaresHelper(n, new HashMap<Integer, Integer>());
}

private int numSquaresHelper(int n, HashMap<Integer, Integer> map) {
    if (map.containsKey(n)) {
        return map.get(n);
    }
    if (n == 0) {
        return 0;
    }
    int count = Integer.MAX_VALUE;
    for (int i = 1; i * i <= n; i++) {
        count = Math.min(count, numSquaresHelper(n - i * i, map) + 1);
    }
    map.put(n, count);
    return count;
}

动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
public int numSquares(int n) {
    int dp[] = new int[n + 1];
    Arrays.fill(dp, Integer.MAX_VALUE);
    dp[0] = 0; 
    //依次求出 1, 2... 直到 n 的解
    for (int i = 1; i <= n; i++) {
        //依次减去一个平方数
        for (int j = 1; j * j <= i; j++) {
            dp[i] = Math.min(dp[i], dp[i - j * j] + 1);
        }
    }
    return dp[n];
}

BFS

BFS 的话，我们可以一层一层的算。第一层依次减去一个平方数得到第二层，第二层依次减去一个平方数得到第三层。直到某一层出现了 0，此时的层数就是我们要找到平方数和的最小个数。

举个例子，n = 12，每层的话每个节点依次减 1, 4, 9…。如下图，灰色表示当前层重复的节点，不需要处理。

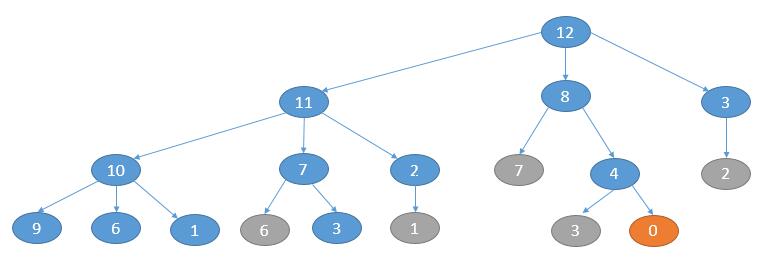
如上图，当出现 0 的时候遍历就可以停止，此时是第 3 层（从 0 计数），所以最终答案就是 3。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public int numSqure(int n){
    Queue<Integer> queue=new LinkedList<>();
    HashSet<Integer> set=new HashSet<>();
    int level=0;
    queue.add(n);
    while(!queue.isEmpty()){
        int size=queue.size();
        level++;
        for(int i=0;i<size;i++){
            int cur=queue.poll();
            for(int j=0;j*j<=n;j++){
                int next=n-j*j;
            }
            if(next==0){
                return level;
            }
            if(!set.contains(next)){
                queue.offer(next);
                set.add(next);
            }
        }
    }
    return -1;
}